Multi Camera Calibration Theory

Multi-Camera Calibration 기사에서 우리는 Multi-Camera Calibration의 실용성에 초점을 맞추었습니다. 이 기사에서 우리는 그 뒤에 숨겨진 몇 가지 이론을 설명할 것입니다.

Calibration object

다중 카메라 보정을 위한 보정 대상은 카메라에 대한 자세(위치 및 방향)를 정확하게 결정할 수 있어야 합니다.

Transformation matrix

행렬 곱을 통해 한 좌표 프레임의 위치 벡터를 다른 좌표 프레임으로 변환하는 데 필요한 회전과 변환을 모두 결합합니다.

The transformation between two cameras

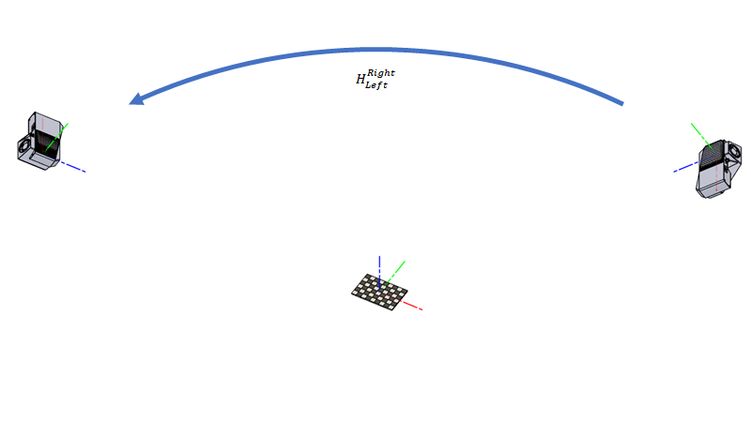
두 대의 카메라가 있는 시나리오를 고려하십시오.

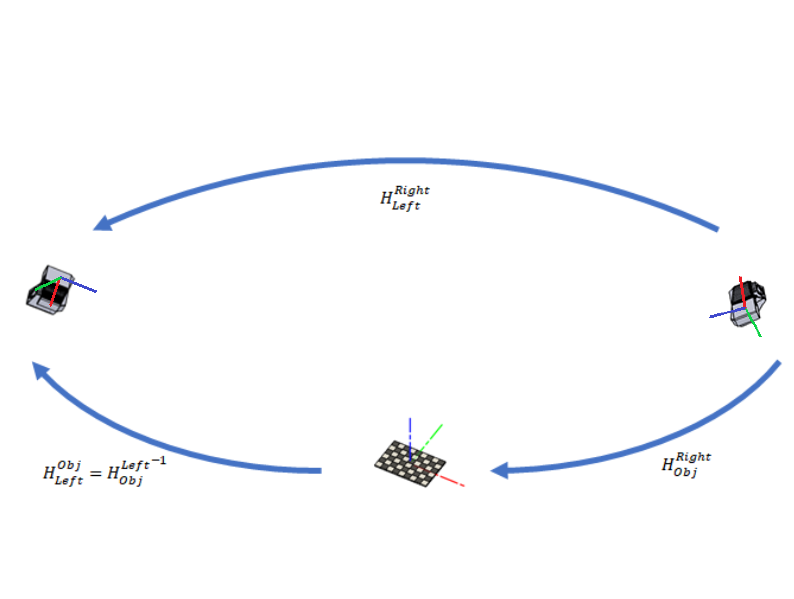
우리는 오른쪽 카메라에서 왼쪽 카메라로의 변환을 설명하는 변환 매트릭스 \(H^{Right}_{Left}\) 를 찾고 있습니다.

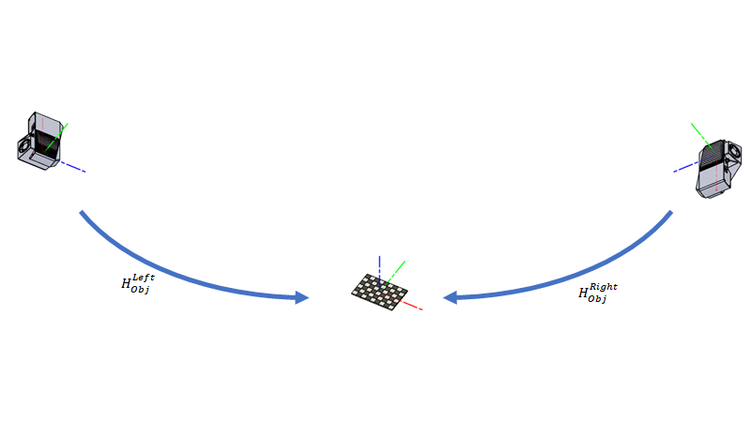
어느 카메라에서 보더라도 카메라 레퍼런스 프레임 \(H^{Obj}_{Left}\) 과 \(H^{Obj}_{Right}\) 에 있는 칼리브레이션 물체의 포즈입니다. 이러한 포즈의 역방향(예: 1)과 (예: 2)을 사용하면 점 구름의 점을 칼리브레이션 개체의 좌표 프레임으로 변환할 수 있습니다.

\[(H^{Obj}_{Left})^{-1} = H_{Obj}^{Left} \qquad (1)\]

\[(H^{Obj}_{Right})^{-1} = H_{Obj}^{Right} \qquad (2)\]

우리는 거기에서 멈추고 최종 결과로 칼리브레이션 대상에 변환 행렬을 제공할 수 있었습니다. 칼리브레이션 객체의 포즈는 종종 임의이기 때문에 종속성을 갖지 않도록 합니다. 따라서 우리는 \(H_{Left}^{Right}\) (예: 3) 또는 \(H^{Left}_{Right}\) 를 원합니다.

\[H_{Left}^{Right} = H_{Obj}^{Right} * H_{Left}^{Obj} = H_{Obj}^{Right} * (H_{Obj}^{Left})^{-1} \qquad (3)\]