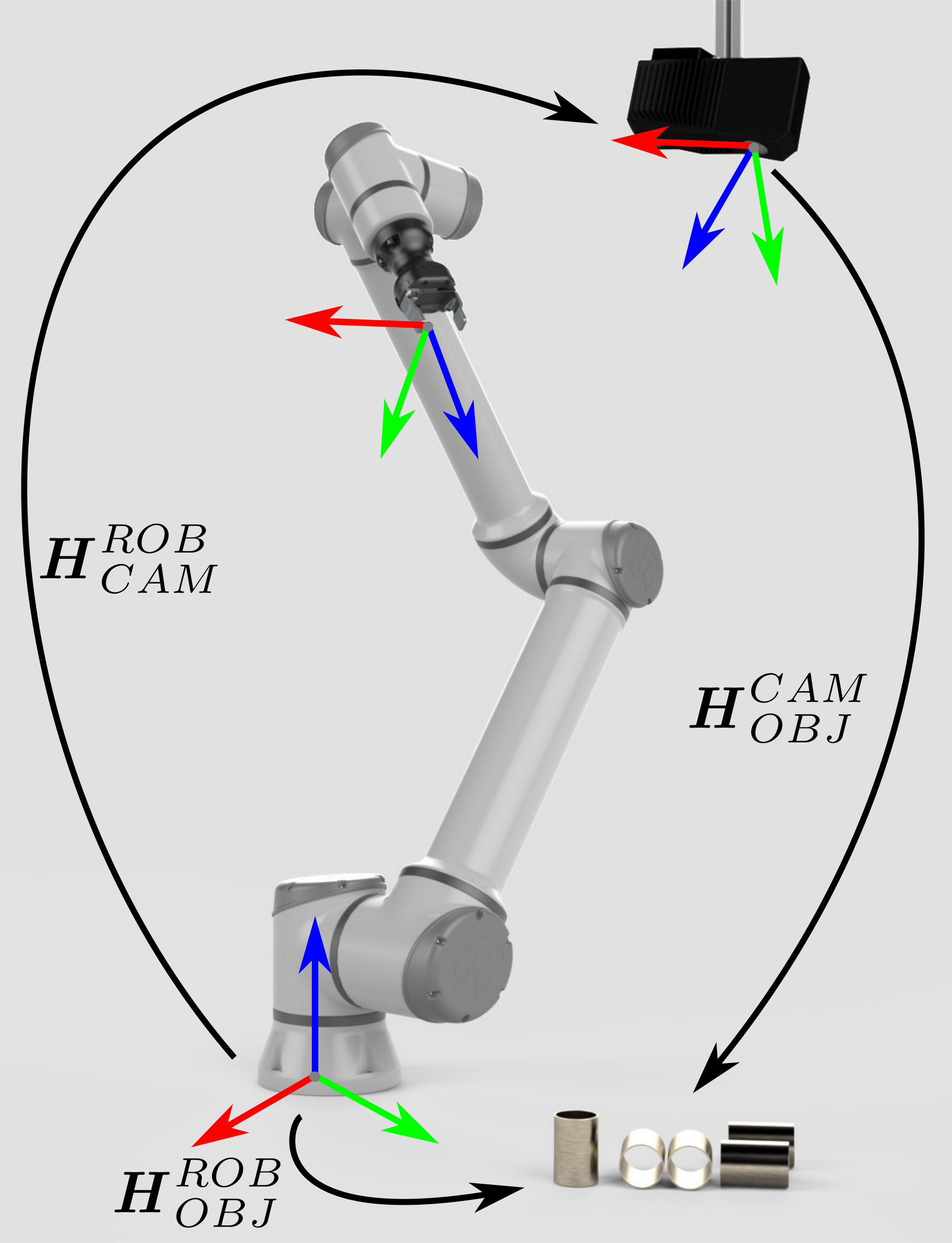
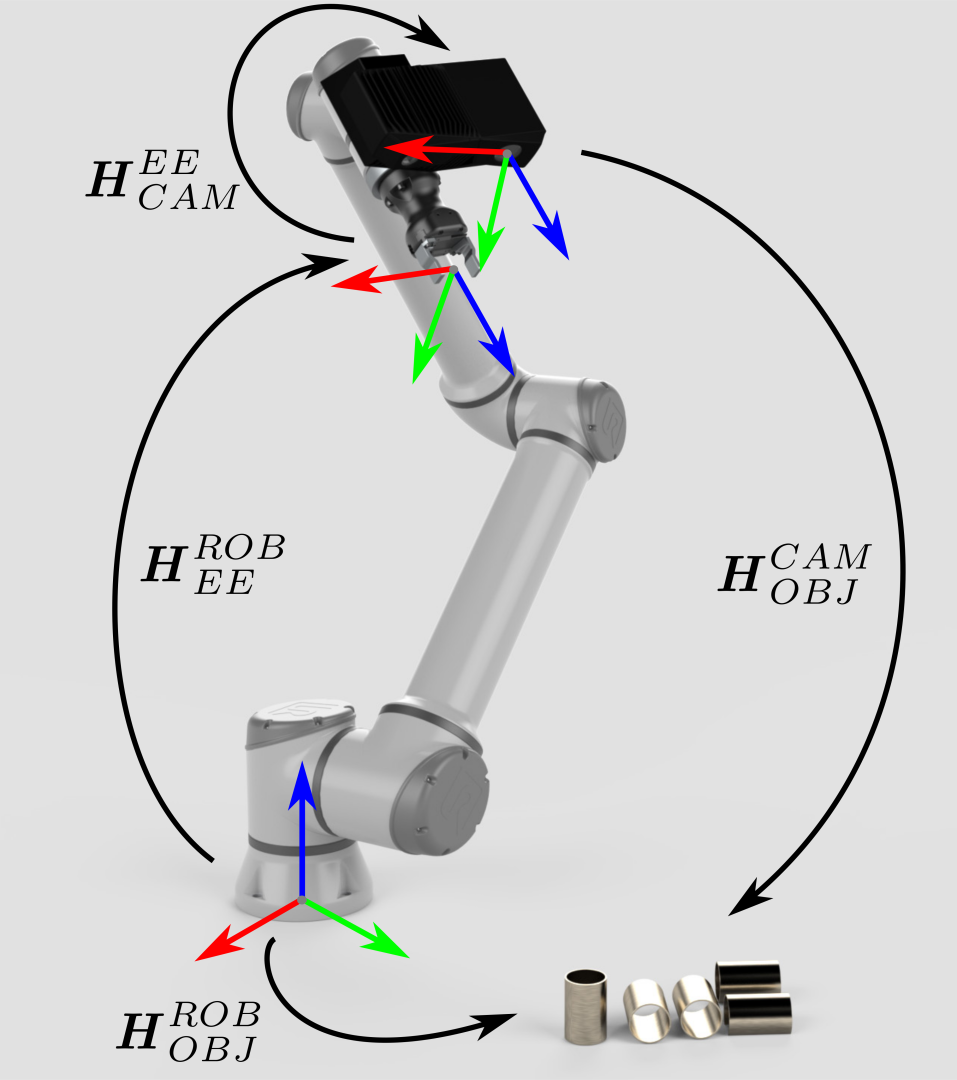
如何使用手眼标定的结果

我们分析了配备Zivid相机和机器视觉软件的机器人拾取物体的应用的要求。可参考 手眼标定的问题。如果您不确定应该如何使用手眼标定的结果，那么您可以在本篇教程中查看到相关信息。我们将介绍如何将对象的坐标从 Zivid 相机坐标系转换到机器人基坐标系。

提示

您可以从我们 的 GitHub 仓库中找到转换3D 点/点云 的 Python 和 C++ 示例。

假设您通过机器视觉软件处理Zivid点云数据，相机检测到目标对象（例如此Zivid测试块），并估计其位置。给出的拾取点的x、y、z的值是对象基于Zivid相机坐标系的坐标值。

小技巧

在运行您的应用之前，建议您使用与手眼标定时相同的捕获周期来 预热 相机。如需进一步降低与温度相关的性能因素的影响，请启用 热稳定功能。

在某些情况下，您的算法还需要输出对象的方向，例如翻转角（roll），俯仰角（pitch）和偏航角（yaw）。 这些参数也是基于Zivid相机的坐标系给出的。

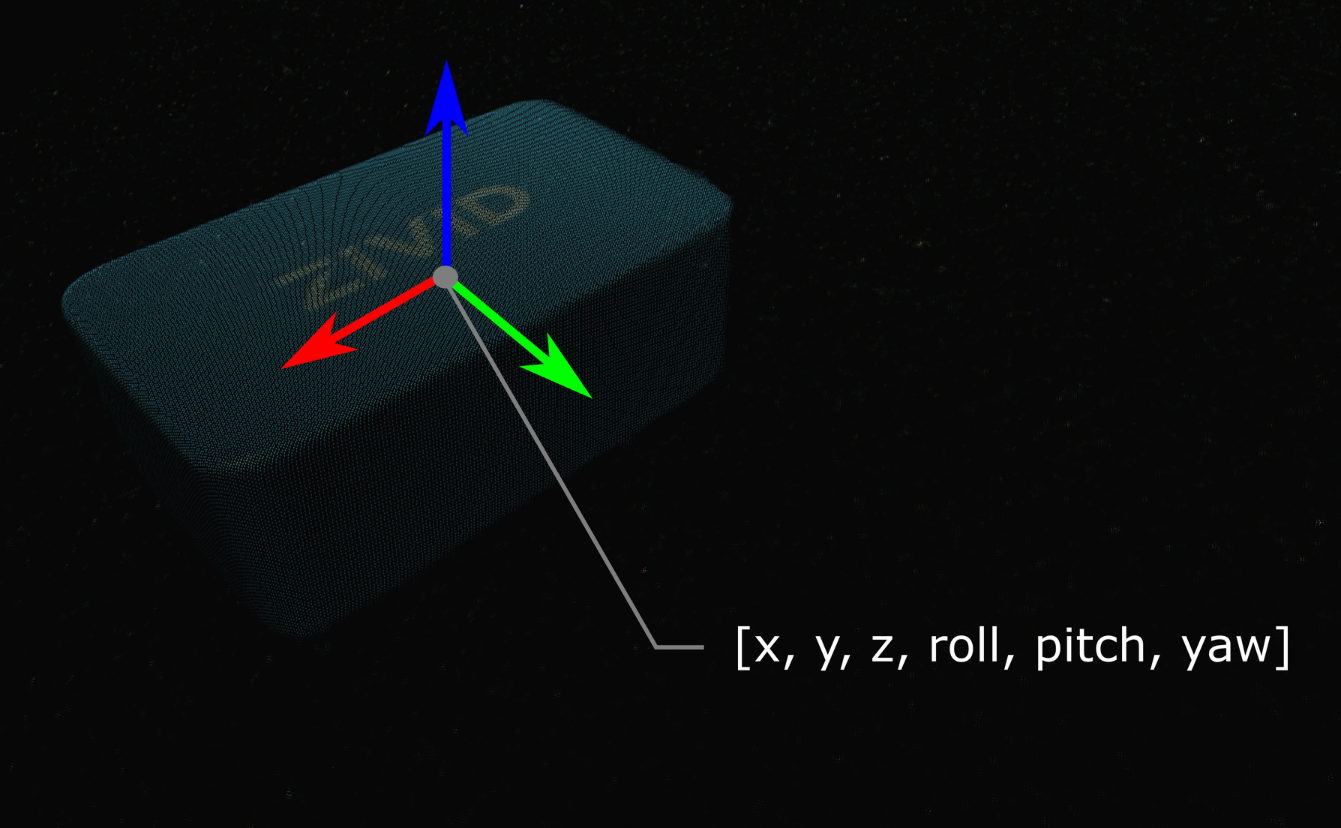
可通过齐次变换矩阵来描述对象的位姿（位置和方向）。 如果您还不熟悉（机器人）位姿和坐标系，请查看 位置、方向和坐标变换。

接下来我们将说明将单个点或整个点云从相机坐标转换到机器人基坐标的数学理论。 实际上，最简单的方法是使用Zivid SDK支持的转换功能。 这会在将数据复制到CPU之前对其进行转换，因此速度非常快。示例 StitchByTransformation 中使用了该功能。

Eye-to-hand

对于eye-to-hand系统，可以通过以下方法将单个3D点从Zivid相机坐标系转换到机器人基坐标系：

\[p^{ROB} = H^{ROB}_{CAM} \cdot p^{CAM}\]

\[\begin{split}\begin{bmatrix} x^{r} \\ y^{r} \\ z^{r} \\ 1 \end{bmatrix} = \begin{bmatrix} \boldsymbol{R}^{r}_{c} & \boldsymbol{t}^{r}_{c} \\ 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} x^{c} \\ y^{c} \\ z^{c} \\ 1 \end{bmatrix}\end{split}\]

如果要将整个Zivid点云从相机坐标系转换到机器人基坐标系，请将上述方程式应用于点云中的每个点。

另一方面，如果要将对象的位姿转换为相对于Zivid相机坐标系的位姿，请应用以下方程式：

\[H^{ROB}_{OBJ} = H^{ROB}_{CAM} \cdot H^{CAM}_{OBJ}\]

\[\begin{split}\begin{bmatrix} \boldsymbol{R}^{r}_{o} & \boldsymbol{t}^{r}_{o} \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} \boldsymbol{R}^{r}_{c} & \boldsymbol{t}^{r}_{c} \\ 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} \boldsymbol{R}^{c}_{o} & \boldsymbol{t}^{c}_{o} \\ 0 & 1 \end{bmatrix}\end{split}\]

请确保位姿是通过齐次变换矩阵表述的。 如果不是，请查看我们的文章 常见的姿态表示方法之间的转换。

由此产生的姿势是机器人工具中心点 (TCP) 应该达到的姿势以进行拾取。 TCP 和机器人法兰之间的偏移量应在机器人侧考虑。

Eye-in-hand

Eye-in-hand系统的方法是类似的。不同之处在于方程式必须包含机器人的当前位姿。同样地，我们假定机器人位姿用齐次变换矩阵表示。如果您的机器人位姿表示方式有所不同，请查看我们关于 常见的姿态表示方法之间的转换 的文章。

以下方程式描述了如何将单个3D点从Zivid相机坐标系转换到机器人基坐标系：

\[p^{ROB} = H^{ROB}_{EE} \cdot H^{EE}_{CAM} \cdot p^{CAM}\]

\[\begin{split}\begin{bmatrix} x^{r} \\ y^{r} \\ z^{r} \\ 1 \end{bmatrix} = \begin{bmatrix} \boldsymbol{R}^{r}_{e} & \boldsymbol{t}^{r}_{e} \\ 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} \boldsymbol{R}^{e}_{c} & \boldsymbol{t}^{e}_{c} \\ 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} x^{c} \\ y^{c} \\ z^{c} \\ 1 \end{bmatrix}\end{split}\]

如果要将整个Zivid点云从相机坐标系转换到机器人基坐标系，请将上述方程式应用于点云中的每个点。

要将对象的位姿转换为相对于Zivid相机坐标系的位姿，请使用以下方程式：

\[H^{ROB}_{OBJ} = H^{ROB}_{EE} \cdot H^{EE}_{CAM} \cdot H^{CAM}_{OBJ}\]

\[\begin{split}\begin{bmatrix} \boldsymbol{R}^{r}_{o} & \boldsymbol{t}^{r}_{o} \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} \boldsymbol{R}^{r}_{e} & \boldsymbol{t}^{r}_{e} \\ 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} \boldsymbol{R}^{e}_{c} & \boldsymbol{t}^{e}_{c} \\ 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} \boldsymbol{R}^{c}_{o} & \boldsymbol{t}^{c}_{o} \\ 0 & 1 \end{bmatrix}\end{split}\]

由此产生的姿势是机器人工具中心点 (TCP) 应该达到的姿势以进行拾取。 TCP 和机器人法兰之间的偏移量应在机器人侧考虑。