You're viewing an old version of the documentation. Click here to see the latest release.

转换

小技巧

我们的网络研讨会 Getting your point cloud ready for your application （为您的应用准备好点云）部分涵盖了转换的相关内容。

介绍

本文介绍了点云转换的背景，如何转换Zivid点云以及为什么这是一个有价值的功能。最后，文章还提供了一个带有代码示例的教程。

Zivid点云是基于 Zivid 相机坐标系 给出的。由于各种原因，不同的应用需要将整个点云或其片段（例如ROI或拾取点）从相机坐标系转换到另一个坐标系。

问题	点云是基于相机坐标系的，但应用需要在另一个坐标系中使用点云数据。
解决方案	将Zivid点云转换到另一个坐标系。

转换 API

一个刚体变换由描述两个坐标系之间的位姿的4×4齐次变换矩阵定义。一旦知道变换矩阵，我们就可以使用Zivid SDK将点云从相机坐标系转换到所需的坐标系。

以下API用于转换点云：

C++C#Python

Zivid::PointCloud::transform(Zivid::Matrix4x4)

小技巧

Zivid SDK允许所有 仿射变换（在欧几里得几何中，仿射变换是保留点、直线和平面的几何变换），包括非刚性变换。这里有一个非刚性变换的例子 通过将点云从mm转换为m来缩放点云。

Transform API使用4x4变换矩阵来转换点云。

C++C#

源

const auto transformMillimetersToMeters =
    Zivid::Matrix4x4{ { 0.001F, 0, 0, 0 }, { 0, 0.001F, 0, 0 }, { 0, 0, 0.001F, 0 }, { 0, 0, 0, 1 } };

转换是在点云上完成的。

C++C#Python

源

pointCloud.transform(transformBaseToCamera);

备注

Zivid SDK中转换API的处理速度非常快，因为它是在GPU中并行完成的，而点云数据此时仍在GPU内存内。使用第三方库计算法线可能更耗时：因为CPU计算通常要慢得多，而GPU计算则需要多出一次数据复制过程。查看 点云捕获过程 了解更多信息。

如需了解更多有关位姿和转换的信息，请查看 位置、方向和坐标变换.

小技巧

• 出于性能原因的考量，可以将转换API与降采样和法线API结合使用，因为GPU执行所有这些计算时， 点云数据仍在GPU内存中时。

• 为了最快地完成数据处理，可以先对点云进行降采样，然后对其进行转换。

• 在转换点云后计算法线，使得法线与点云在同一坐标系中。

应用中的转换

本节将介绍使用点云转换功能的Zivid相机和机器人的应用。这里说明了这些应用中的典型坐标系以及为什么要将点云转换到这些坐标系里。

抓取

为了让机器人能够拾取在点云中检测到的物体，点云的坐标必须从相机坐标系转换到机器人可以理解的坐标系。

机器人坐标系

我们通常希望将对象坐标或整个点云转换到机器人基础坐标系。您可以从这篇文章了解详细说明 如何使用手眼标定的结果.

平面坐标系

相机通常与抓取面不平行。转换点云使点云z轴与平面z轴匹配有助于我们更好地理解和解析点云数据。因此，通常会将点云转换到抓取面所在的坐标系，例如料箱底层或传送带。

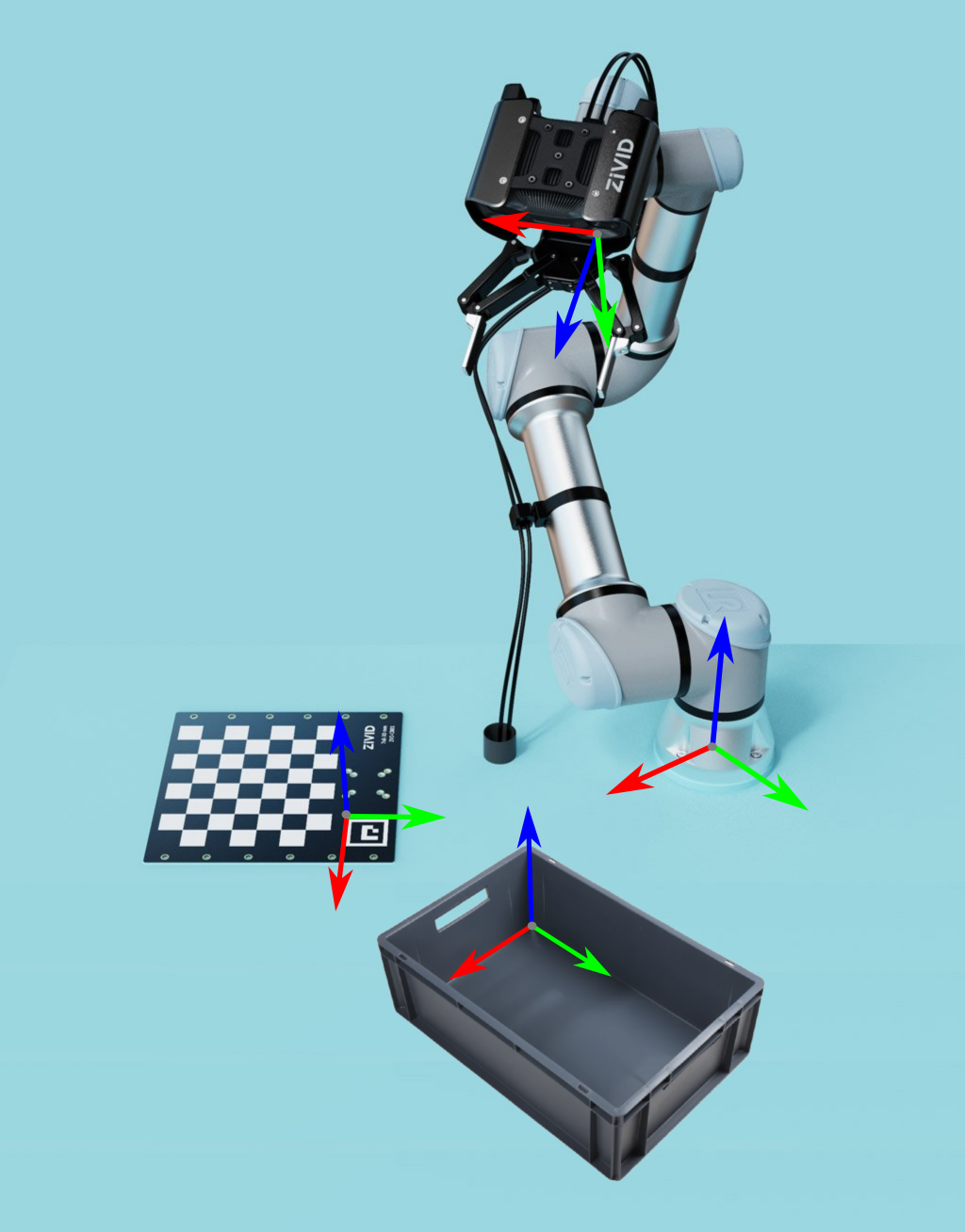
料箱坐标系

还有一个步骤可以帮助我们更好地理解点云数据并评估抓取表现。即将点云的x轴和y轴与料箱的x轴和y轴对齐。

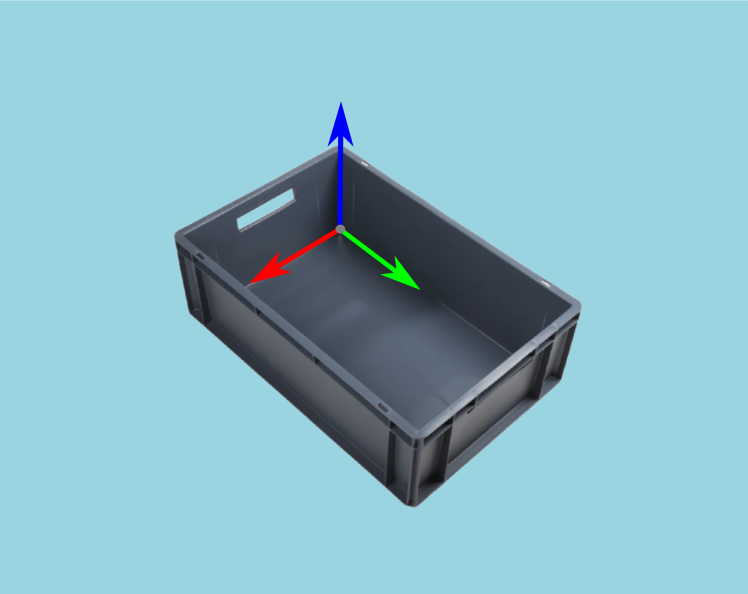
感兴趣区域

相机视野通常大于我们的感兴趣区域 (ROI)，例如料箱。因此，将料箱轴与点云轴对齐的另一个原因是它可以让我们在料箱周围设置一个ROI框。然后，我们可以根据ROI裁剪点云，以仅获取料箱范围内的点。

小技巧

较小的点云可以使检测更快，总抓取周期时间更短。

For an implementation example, check out ROI box filter via Checkerboard. This tutorial demonstrates how to filter the point cloud transformed to the Checkerboard coordinate system based on a ROI box given relative to the checkerboard. We also have 通过ArUco标记实现的ROI框过滤器 tutorial where instead of the checkerboard we use the ArUco marker.

拼接

点云拼接通常涉及将点云转换到不同的坐标系。

多个固定安装的相机

Zivid 多相机标定 能够将来自多个相机的点云转换到其中一台相机（主相机）的坐标系中。在多相机标定中，我们通常希望将拼接后的点云转换到一个不同的坐标系中，比如对象坐标系。

单个手臂安装的相机

通过相机安装在手臂上的配置，您可以使用同一相机从多个角度拍摄多个点云用于拼接。一旦点云在主相机坐标系中完成拼接后，就可以方便地将其转换到对象坐标系。

单相机和转盘

如果我们知道转盘相对于相机的位姿，我们可以拼接点云并将它们转换到转盘坐标系。

备注

多相机标定 是 SDK 的一部分，它使用 Zivid 标定板.

位姿估计

获取相机相对于机器人基坐标系的位姿是通过 手眼标定 实现的。如果我们需要相对于任意用户定义的坐标系的位姿，我们可以在场景中放置标定对象，例如基准标记和棋盘格。由于我们知道它们的几何形状，因此估计它们的位姿相对简单。

For an implementation example, check out Transform via Checkerboard. This tutorial demonstrates how to estimate the pose of the checkerboard and transform a point cloud using a 4x4 homogeneous transformation matrix to the checkerboard coordinate system. We also have 基于ArUco标记的坐标转换 tutorial where instead of the checkerboard we use the ArUco marker.

版本历史

SDK	变更
2.0.0	添加了转换API。