多相机标定的理论
在多相机标定一文中,我们重点介绍了多相机标定的实际操作。在本文中,我们将解释一些相关的理论。
标定对象
用于多台相机标定的标定对象必须满足可以准确地确定其相对于相机的位姿(位置和方向)。
变换矩阵
组合了旋转和平移的矩阵,可使用该矩阵通过矩阵乘法将一个坐标系中的位置矢量转换到另一坐标系。
两台相机之间的转换
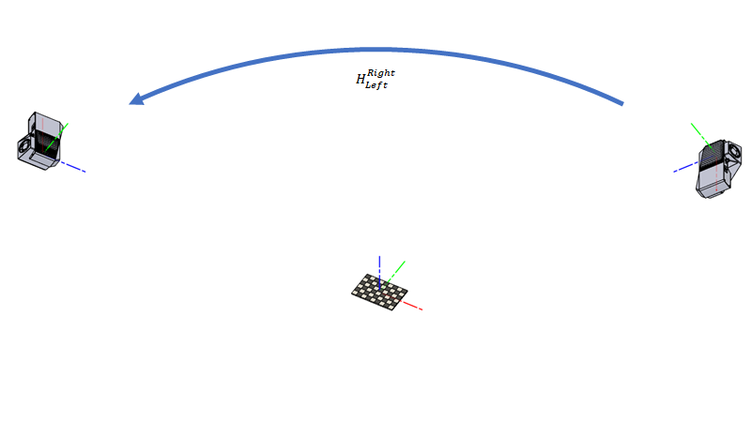
考虑使用两台相机的场景。

我们想找到描述了从右侧相机转换到左侧相机坐标系的变换矩阵 \(H^{Right}_{Left}\) 。
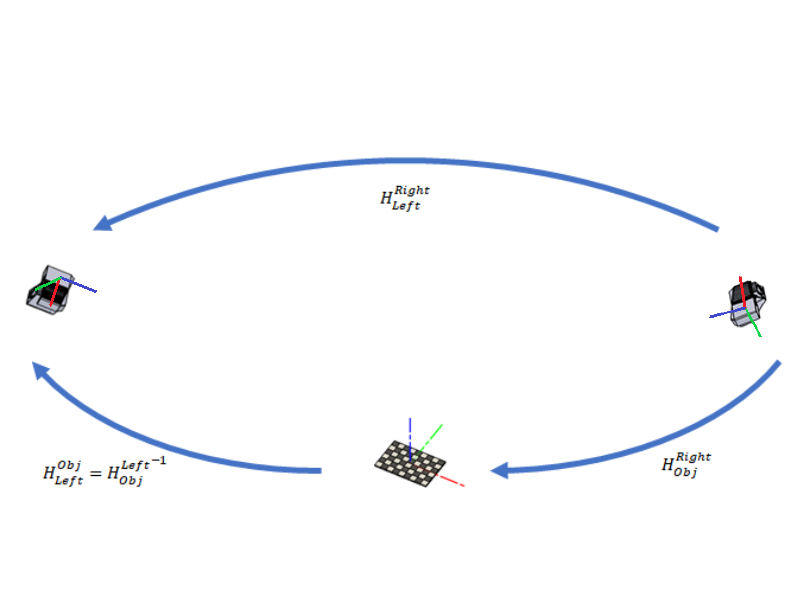
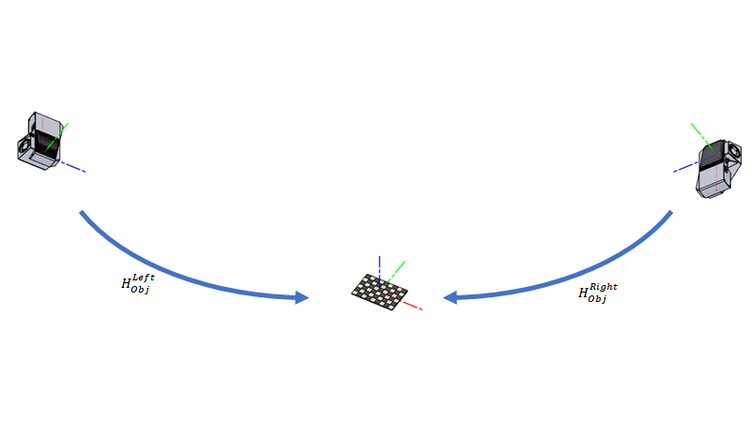
但是,我们从每个相机获得的数据都是标定对象在该相机参考坐标系中的位姿, \(H^{Obj}_{Left}\) 和 \(H^{Obj}_{Right}\)。这些位姿的倒数,(eq. 1) 和 (eq. 2),允许将点云中的点转换到标定对象的坐标系。
\[(H^{Obj}_{Left})^{-1} = H_{Obj}^{Left} \qquad (1)\]
\[(H^{Obj}_{Right})^{-1} = H_{Obj}^{Right} \qquad (2)\]
我们本可以在这里结束,将相对于标定对象的变换矩阵作为最终结果。但是我们不想依赖于标定对象的位姿,因为这个位姿通常是随机的。因此我们想要得到 \(H_{Left}^{Right}\) (eq. 3) 或 \(H^{Left}_{Right}\)。
\[H_{Left}^{Right} = H_{Obj}^{Right} * H_{Left}^{Obj} = H_{Obj}^{Right} * (H_{Obj}^{Left})^{-1} \qquad (3)\]