Downsampling Theory

Introduction

This article explains the theory on how to downsample a Zivid point cloud. If you are interested in the SDK implementation, go to Downsample article.

Why Not Keep Every Nth Pixel?

When downsampling an image, the goal is to reduce the size of the image while preserving as much of the quality as possible.

A common approach to downsampling is to keep every second, third, fourth, etc., pixel and discard the rest. However, this is not necessary ideal because of colors filters on the sensor. Take the Bayer filter mosaic as an example. The Bayer filter mosaic grid for a 4x4 image is shown below.

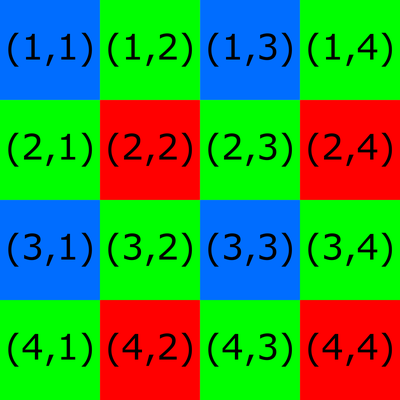
Note

Zivid point clouds coordinate system start with (0,0).

With this filter, each pixel on the camera corresponds to one color filter on the mosaic.

Consider a downsampling algorithm that keeps every other pixel. All kept pixels would correspond to the same color filter:

• (1,1) (1,3) (3,1) (3,3) → Blue

• (2,1) (2,3) (4,1) (4,3) → Green

• (1,2) (1,4) (3,2) (3,4) → Green

• (2,2) (2,4) (4,2) (4,4) → Red

Recommended Downsampling Procedure

To preserve data quality, you should consider all pixels and perform downsampling on an even pixel grid (2x2, 4x4, 6x6, etc.). Here is a recommended procedure to reduce the image size by half, e.g., from 4x4 to 2x2.

Downsampling RGB values (color image)

Calculate each pixel value of the new image by averaging every 2x2 pixel grid of the initial image for each channel R, G, and B. For example, to calculate the new R values:

\[\begin{split}\begin{align} R_{new}(1,1) = \frac{R(1,1)+R(1,2)+R(2,1)+R(2,2)}{4}\\ R_{new}(1,2) = \frac{R(1,3)+R(1,4)+R(2,3)+R(2,4)}{4}\\ R_{new}(2,1) = \frac{R(3,1)+R(3,2)+R(4,1)+R(4,2)}{4}\\ R_{new}(2,2) = \frac{R(3,3)+R(3,4)+R(4,3)+R(4,4)}{4} \end{align}\end{split}\]

Repeat the same process for G and B values.

Downsampling XYZ values (point cloud)

For point cloud data, we also need to handle NaN values. As with R, G, B color values, X, Y, Z pixel values of the new image should be calculated by taking every 2x2 pixel grid of the initial image. Instead of a normal average, use an SNR-weighted average value for each coordinate. To brush up on how Zivid uses SNR check out our SNR page.

There are cases where the X, Y, Z coordinates of any pixel may have a NaN value, but the SNR for that pixel will not be NaN. We can handle this by doing a basic check to see if any pixel has a NaN value for one of its coordinates. Check if any pixel has a NaN value for one of the X, Y, Z coordinates. If it does, then replace the SNR value for that pixel with zero. This can be done by selecting the pixels whose e.g. Z coordinates are NaNs and setting their SNR value to zero:

\[SNR(isNAN(Z)) = 0\]

where \(isNAN()\) is a logical masking function that selects only the pixels whose input coordinates are NaNs.

The next step is calculating the sum of SNR values for every 2x2 pixel grid:

\[C_{sum}=SNR(1,1) + SNR(1,2) + SNR(2,1) + SNR(2,2)\]

After this, calculate the weight for each pixel of the initial image:

\[\begin{split}\begin{align} W(1,1) = \frac{SNR(1,1)}{C_{sum}}\\ W(1,2) = \frac{SNR(1,2)}{C_{sum}}\\ W(2,1) = \frac{SNR(2,1)}{C_{sum}}\\ W(2,2) = \frac{SNR(2,2)}{C_{sum}} \end{align}\end{split}\]

To avoid having to deal with \(NaN \cdot 0 = NaN\) instead of \(NaN \cdot 0 = 0\) it is advisable to do the following:

\[\begin{split}\begin{align} & W(isNaN(W)) = 0 \\\\ & X(isNaN(X)) = 0 \\\\ & Y(isNaN(Y)) = 0 \\\\ & Z(isNaN(Z)) = 0 \end{align}\end{split}\]

Finally, the X, Y, Z coordinate values can be calculated. Here is an example for calculating the new X:

\[X_{new}(1,1) = X(1,1) \cdot W(1,1) + X(1,2) \cdot W(1,2) + X(2,1) \cdot W(2,1) + X(2,2) \cdot W(2,2)\]

The same should be done for Y and Z values.