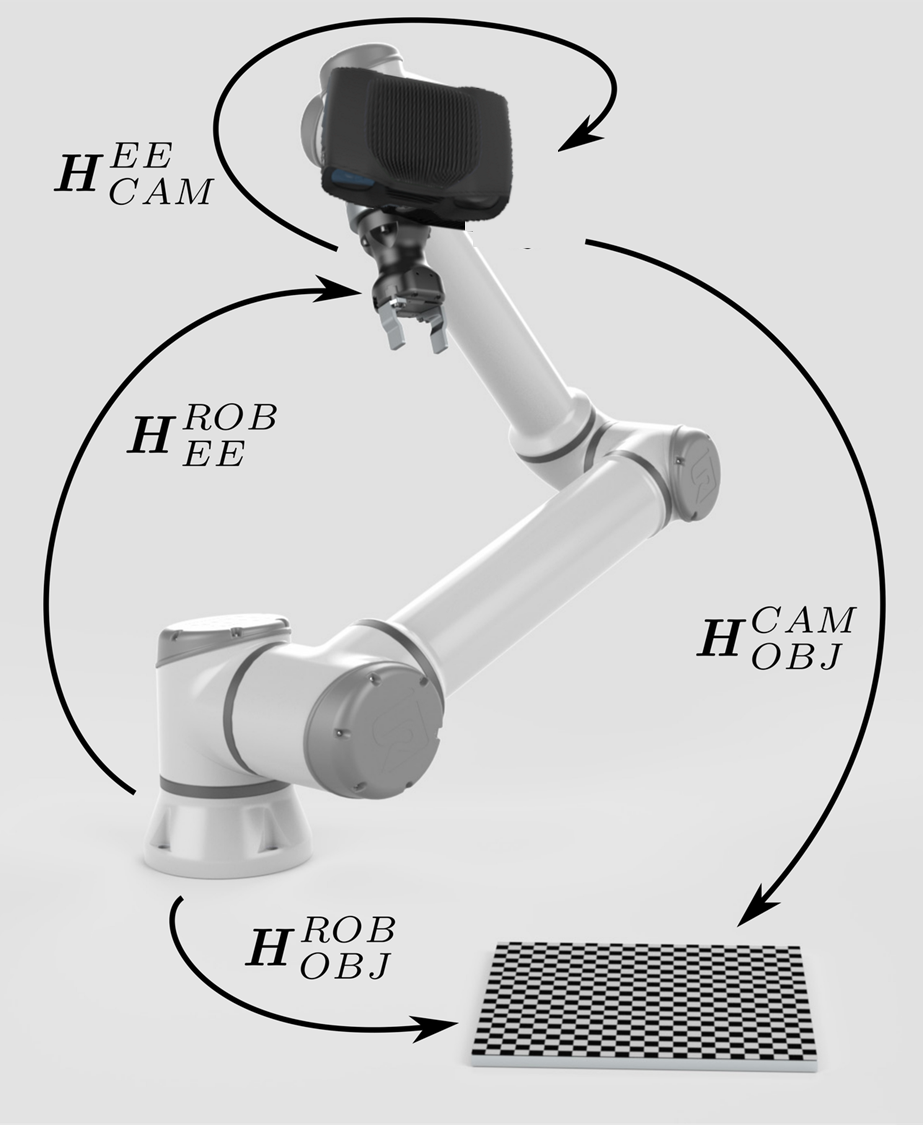
Hand-Eye Calibration Solution

The previous part of this tutorial presented the problem that the hand-eye calibration needs to solve. This tutorial describes the background idea for a solution. The core idea is the same for eye-to-hand systems and eye-in-hand systems. Therefore, we first provide a detailed solution for the eye-to-hand configuration. Then, we point out the differences in the eye-in-hand configuration.

Note

You don’t need a tool, or to know its pose (if you have one attached ) to do the hand-eye calibration. The Tool Center Point (TCP) value does not affect the hand-eye calibration result. In this article and later tutorials, the end-effector refers to the tool flange/end-link.

Eye-to-hand

How to solve the eye-to-hand calibration?

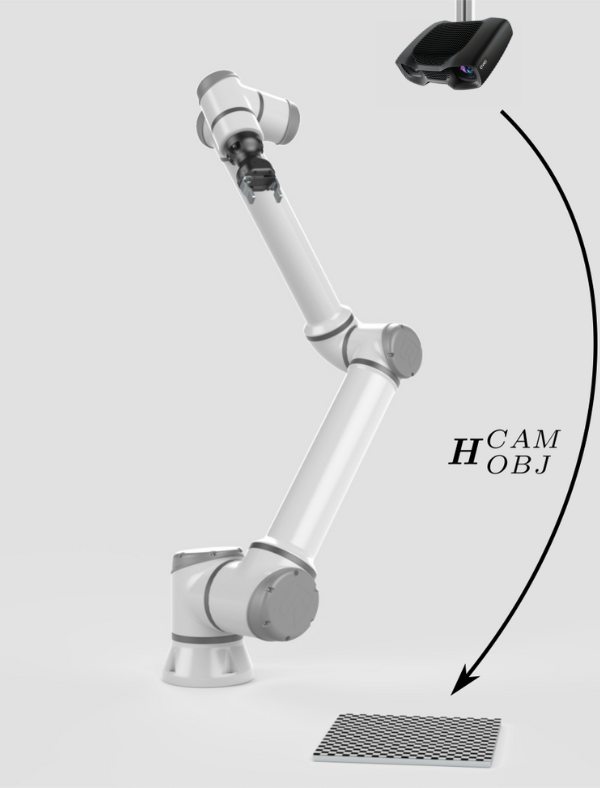
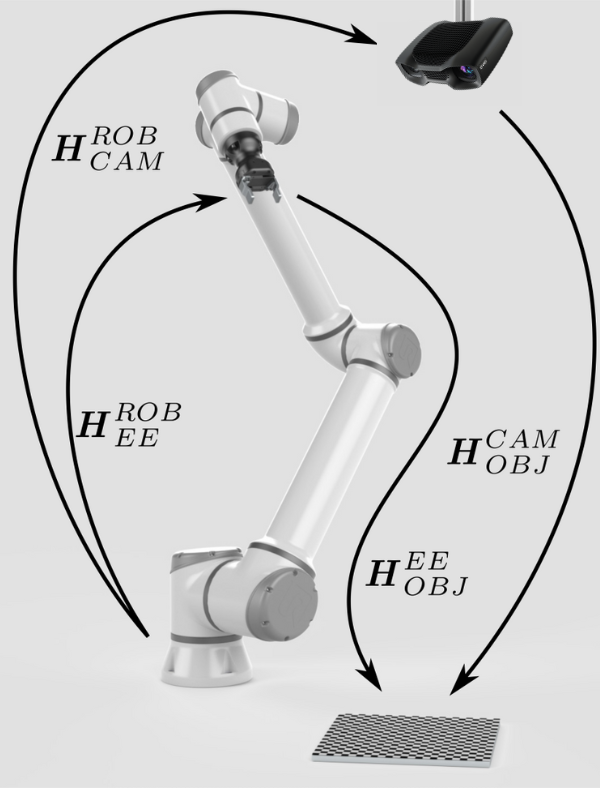
The first step is choosing a calibration object, e.g. a checkerboard. Zivid calibration objects (checkerboards and ArUco markers) will be covered in the next part of this tutorial.
The calibration object is of known geometry. Thus, it can be detected from the camera image. Further, its pose relative to the camera (\(H^{CAM}_{OBJ}\)) can be estimated.
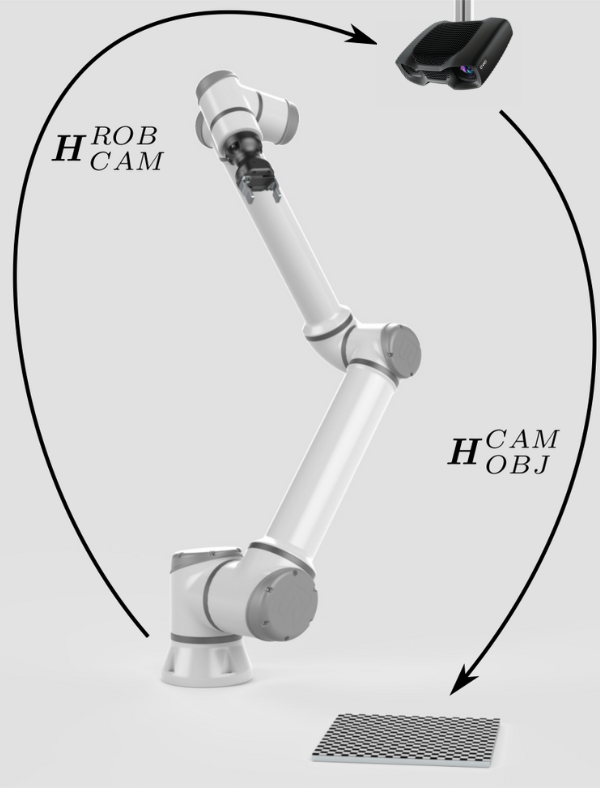
To calculate the relative pose between the camera and the robot (\(H^{ROB}_{CAM}\)), we somehow need to close the circle between the poses.
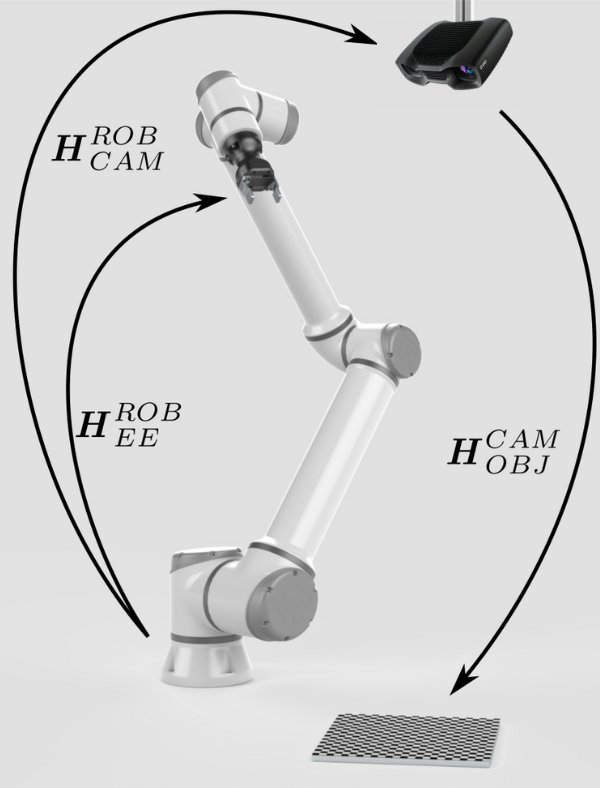
The pose of the end-effector relative to the robot base (\(H^{ROB}_{EE}\)) is also known, provided by the robot controller.
The missing pose that will close the pose circle is the pose of the object relative to the end-effector (\(H^{EE}_{OBJ}\)).
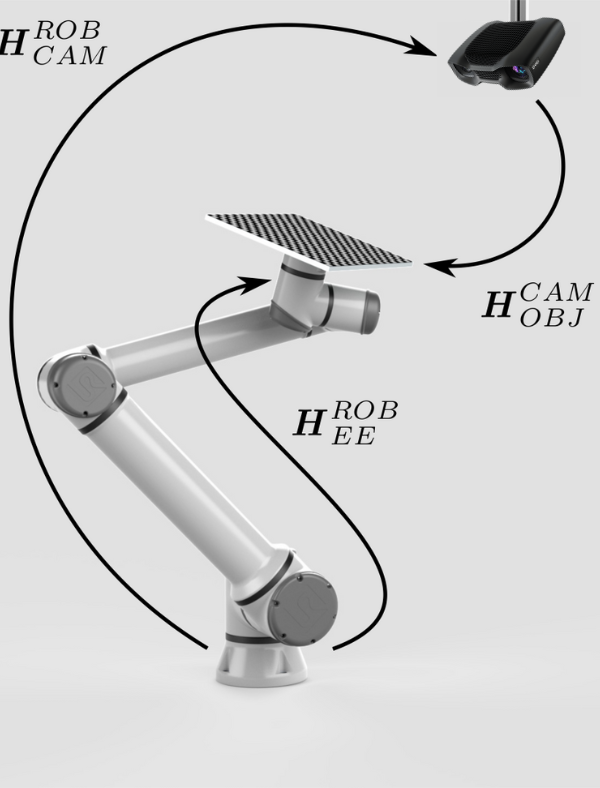
To get ‘rid’ of this pose or ‘fix’ it, we can mount the calibration object onto the end-effector.
Now it seems we have everything to close the pose circle and thus calculate the pose of the camera relative to the robot (\(H^{ROB}_{CAM}\)). However, it is not that simple.
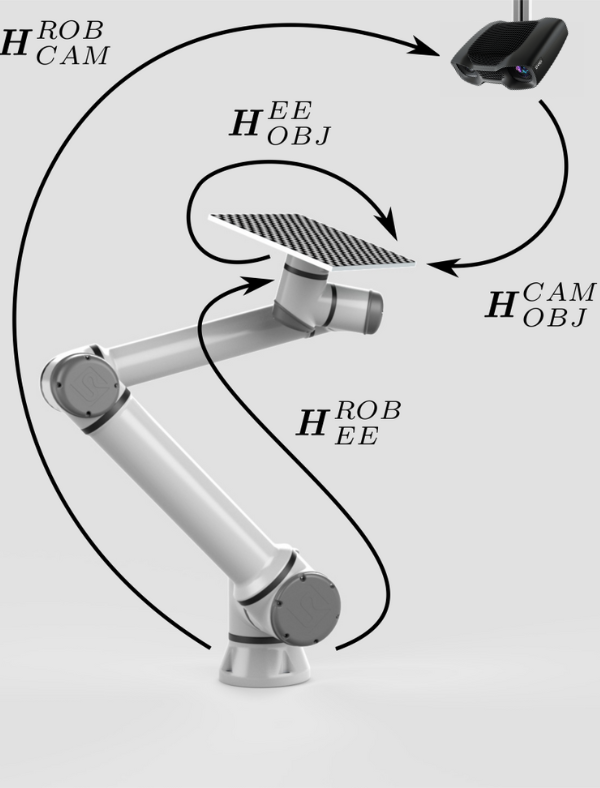
This is because we haven’t really got ‘rid’ of the relative pose (\(H^{EE}_{OBJ}\)). However, we have made it constant. Now, \(H^{EE}_{OBJ}\) will not change during the motion of the robot. This enables us to move a robot to a set of different postures. For each one, \(H^{ROB}_{CAM}\) can be expressed as a function of the remaining two variable, known poses: Robot to end-effector \(H^{ROB}_{EE}\) Camera to calibration object \(H^{CAM}_{OBJ}\) and one constant, unknown pose \(H^{EE}_{OBJ}\). With this set of equations, it is possible to utilize an optimization technique, such as Tsai’s method, to calculate the desired pose \(H^{ROB}_{CAM}\).

Eye-in-hand

How to solve the eye-in-hand calibration?

The situation is very similar for eye-in-hand systems. In this case the calibration object is fixed to the work environment. Thus, it is ensured that its pose relative to the robot base is constant during the robot motion.
This allows us to express the pose of the camera relative to the end-effector (\(H^{EE}_{CAM}\)) as a function of two variable, known poses: Robot to end-effector \(H^{ROB}_{EE}\) Camera to calibration object \(H^{CAM}_{OBJ}\) and one constant, unknown pose \(H^{ROB}_{OBJ}\). Just as in the eye-to-hand configuration case, we can solve for \(H^{EE}_{CAM}\).

Now that we’ve explained how to solve the hand-eye calibration problem, let’s see learn about Calibration Object.