降采样理论

介绍

本文介绍如何在不使用Zivid SDK的情况下对Zivid点云进行降采样。

备注

从Zivid SDK v2.1.0开始，降采样可通过Zivid API实现。

如果您对SDK实现的方法感兴趣，请查看 降采样。

对点云进行降采样可能会决策保留初始的结构点云中的第二，第三，第四等像素，而丢弃所有其他像素。但是，对于Zivid相机，这并不是最佳解决方案。原因是我们的相机传感器有一个 拜耳滤镜马赛克。下图显示了4 x 4图像的Bayer滤镜马赛克的网格图案。相机图像上的每个像素对应马赛克上的一个颜色过滤器。网格图案中的数字代表图像坐标。请注意，某些图像坐标系，例如我们API中的坐标系，以(0,0)开头。

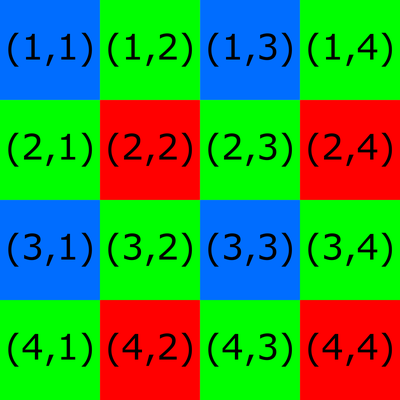
图像传感器像素阵列上彩色滤光片的拜耳排列。

考虑一种保留所有其他像素的降采样算法。对于所有四个可能的选项，所有保留的像素将对应于相同的颜色过滤器：

  • (1,1) (1,3) (3,1) (3,3) → 蓝色

  • (2,1) (2,3) (4,1) (4,3) → 绿色

  • (1,2) (1,4) (3,2) (3,4) → 绿色

  • (2,2) (2,4) (4,2) (4,4) → 红色

为了保证数据质量，在对点云进行降采样时应该考虑所有像素。此外，应基于对原始图像的偶数像素网格（2x2、4x4、6x6等）执行的过程来获得降采样图像的每个像素。建议按以下说明对Zivid点云进行降采样操作， 假定目标是将点云尺寸减少一半，比如从4x4到2x2。

拜耳网格降采样。

降采样RGB值（彩色图像）

新图像的每个像素值应由初始图像的每个2x2像素网格的平均值计算得出。应该对每个通道的 R、G 和 B 执行此操作。下面是一个计算新 R 值的示例：

\[\begin{split}\begin{align} R_{new}(1,1) = \frac{R(1,1)+R(1,2)+R(2,1)+R(2,2)}{4}\\ R_{new}(1,2) = \frac{R(1,3)+R(1,4)+R(2,3)+R(2,4)}{4}\\ R_{new}(2,1) = \frac{R(3,1)+R(3,2)+R(4,1)+R(4,2)}{4}\\ R_{new}(2,2) = \frac{R(3,3)+R(3,4)+R(4,3)+R(4,4)}{4} \end{align}\end{split}\]

执行相同的操作来计算 G 和 B 的值。

用于计算 R、G、B 值的程序也可用于计算新的降采样点云的 X、Y、Z 的值。但是在计算 X、Y、Z 值时，还需要处理点云中的NaN值。因此，前面的方法并不是最佳的解决方案，下面将介绍一种更好的方法。

降采样XYZ值（点云）

X, Y, Z 新图像的像素值应通过获取初始图像的每个2x2像素网格来计算。每个坐标应使用 SNR 加权平均值，而不是正常平均值。如需了解Zivid是如何使用SNR的，请查看 SNR页面。

在某些情况下，任何像素的 X、Y、Z 坐标都可能为NaN值，但该像素的 SNR 不会是NaN。我们可以通过做一个基本的检查来查看任何像素的坐标之一是否有NaN值，从而解决这个问题。查看是否有任何一个像素的 X、Y、Z 坐标中的任何一个值为NaN值。如果是，则将该像素的 SNR 值替换为0。这可以通过筛选像素来完成，例如将 Z 坐标为NaN的像素筛选出来，并将它们的 SNR 值设置为0：

\[SNR(isNAN(Z)) = 0\]

\(isNAN()\) 是一个逻辑屏蔽函数，它将仅筛选出输入坐标为NaN的像素。

下一步是计算每个2x2像素网格的 SNR 值的总和：

\[C_{sum}=SNR(1,1) + SNR(1,2) + SNR(2,1) + SNR(2,2)\]

然后计算初始图像的每个像素的权重：

\[\begin{split}\begin{align} W(1,1) = \frac{SNR(1,1)}{C_{sum}}\\ W(1,2) = \frac{SNR(1,2)}{C_{sum}}\\ W(2,1) = \frac{SNR(2,1)}{C_{sum}}\\ W(2,2) = \frac{SNR(2,2)}{C_{sum}} \end{align}\end{split}\]

为了避免不得不处 理 \(NaN \cdot 0 = NaN\) 代替 \(NaN \cdot 0 = 0\)，建议执行以下操作：

\[\begin{split}\begin{align} & W(isNaN(W)) = 0 \\\\ & X(isNaN(X)) = 0 \\\\ & Y(isNaN(Y)) = 0 \\\\ & Z(isNaN(Z)) = 0 \end{align}\end{split}\]

最后可以计算出 X、Y、Z 坐标值。以下是计算新 X 的示例：

\[X_{new}(1,1) = X(1,1) \cdot W(1,1) + X(1,2) \cdot W(1,2) + X(2,1) \cdot W(2,1) + X(2,2) \cdot W(2,2)\]

对 Y 和 Z 的值也执行同样的操作。

请注意，在示例代码中，虽然底层概念相同，但操作顺序与上述内容略有不同：

\[X_{new}(1,1) = \frac{X(1,1) \cdot SNR(1,1) + X(1,2) \cdot SNR(1,2) + X(2,1) \cdot SNR(2,1) + X(2,2) \cdot SNR(2,2)}{C_{sum}}\]