Multi Camera Calibration Theory
In the Multi-Camera Calibration article, we focused on the practicalities of Multi-Camera Calibration. In this article, we will explain some of the theory behind.
Calibration object
The calibration object for multi-camera calibration must be such that it is possible to accurately determine its pose (position and orientation) relative to a camera.
Transformation matrix
Combines both rotation and translation required to transform a position vector in one coordinate frame to another coordinate frame via matrix multiplication.
The transformation between two cameras
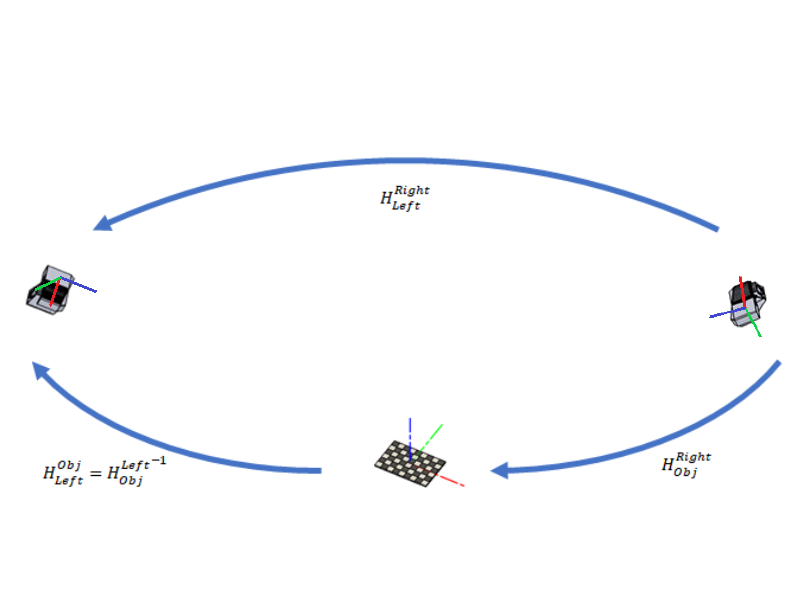
Consider the scenario with two cameras.

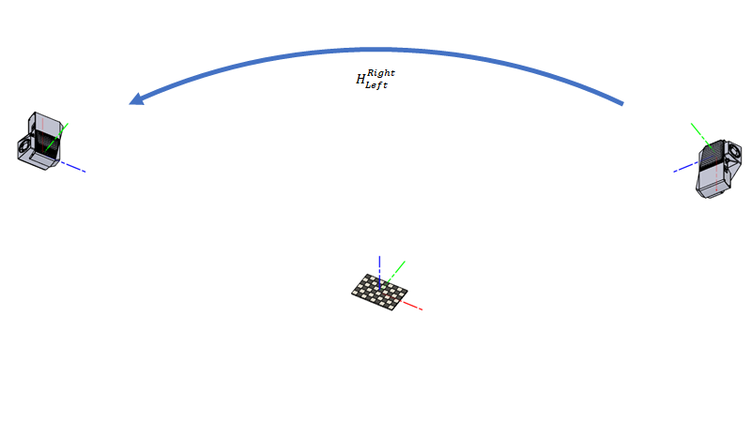
We want to find the transformation matrix \(H^{Right}_{Left}\) which describes the transformation from the camera on the right to the camera on the left.
What we have though, from either camera, is the pose of the calibration object in the camera reference frame \(H^{Obj}_{Left}\) and \(H^{Obj}_{Right}\). The inverse of these poses, (eq. 1) and (eq. 2), allows the transformation of the points in the point clouds to the calibration objects’ coordinate frame.
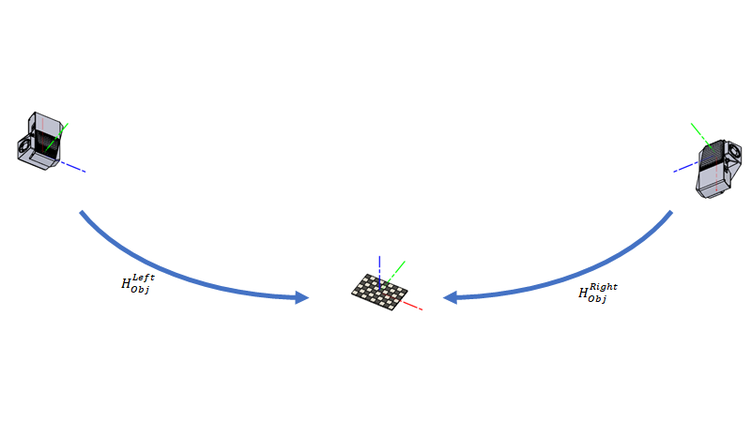
We could have stopped there, and provided transformation matrices to the calibration object, as a final result. We do not want to have a dependency on the pose of the calibration object, as that is often arbitrary. Thus we want either \(H_{Left}^{Right}\) (eq. 3) or \(H^{Left}_{Right}\).