Aperture
Introduction

The camera aperture is the opening of the lens window. Some cameras come with a fixed aperture, while others are adjustable. The aperture size is typically described in \(f\)-numbers, which can at times be counter intuitive, since the area of the opening increases as the \(f\)-number decreases. The \(f\)-number \(N\) is given by:
where \(f\) is the focal length and \(D\) is the diameter of the entrance pupil. The focal length is the distance from the lens to the focal point F inside the camera. Most modern lenses use a standard \(f\)-number. This is based on the geometric sequence of numbers that correspond to the powers of the square root of 2: \(\frac{f}{\sqrt{2^n}}\). This way, the area of the pupil is reduced by half for every decrement of this geometric series. Thus, stepping up or down this series corresponds to adding or subtracting stops.
Aperture in Zivid cameras
Zivid cameras have an integrated electro-mechanical iris that can be rapidly adjusted. A completely open pupil corresponds to an \(f\)-number of \(\frac{f}{1.4}\) and a completely closed pupil to an \(f\)-number of \(\frac{f}{32}\). To use the stop method, it is recommended to use the following f-number values:
\(f\)-number |
\(\frac{f}{1.4}\) |
\(\frac{f}{2}\) |
\(\frac{f}{2.8}\) |
\(\frac{f}{4}\) |
\(\frac{f}{5.6}\) |
\(\frac{f}{8}\) |
\(\frac{f}{11}\) |
\(\frac{f}{16}\) |
\(\frac{f}{22}\) |
\(\frac{f}{32}\) |
Stops |
+4 |
+3 |
+2 |
+1 |
0 |
-1 |
-2 |
-3 |
-4 |
-5 |
Aperture and Depth-of-Field
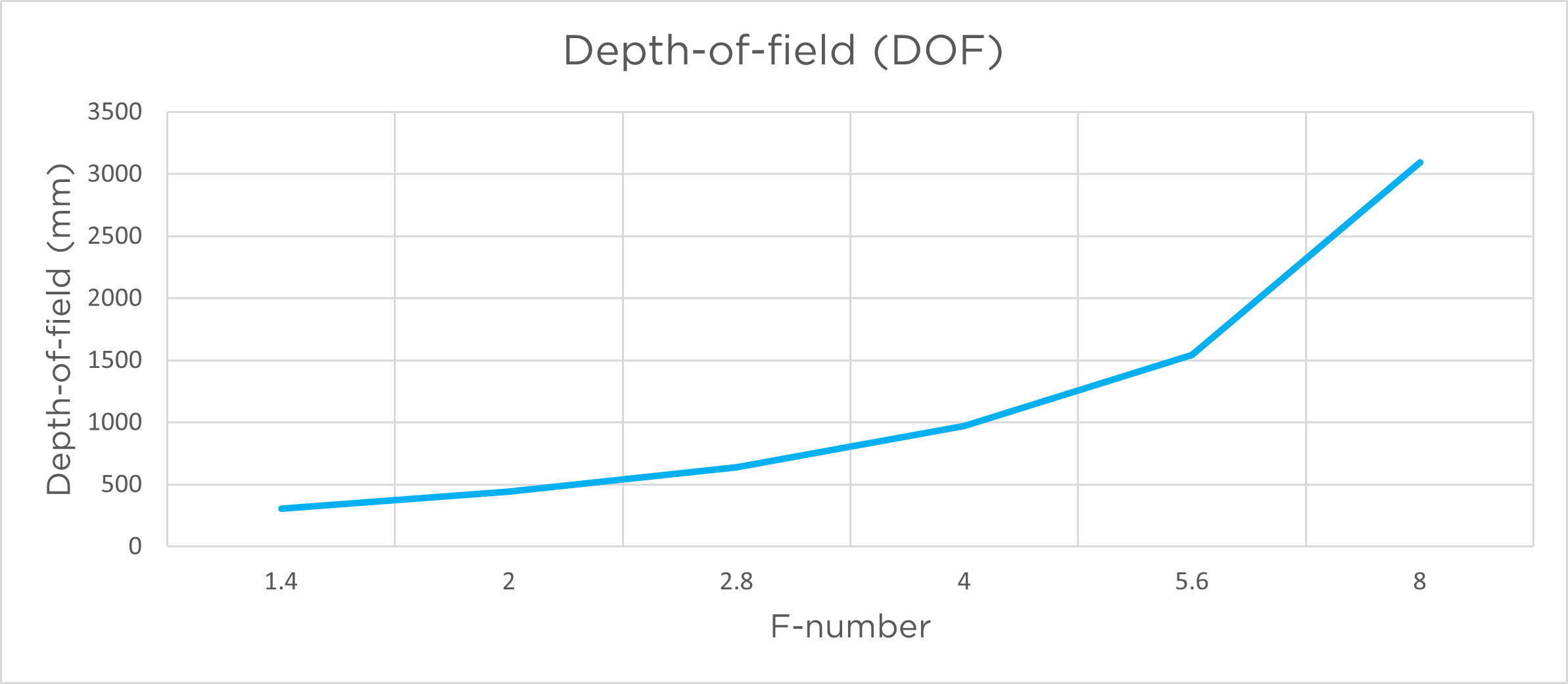
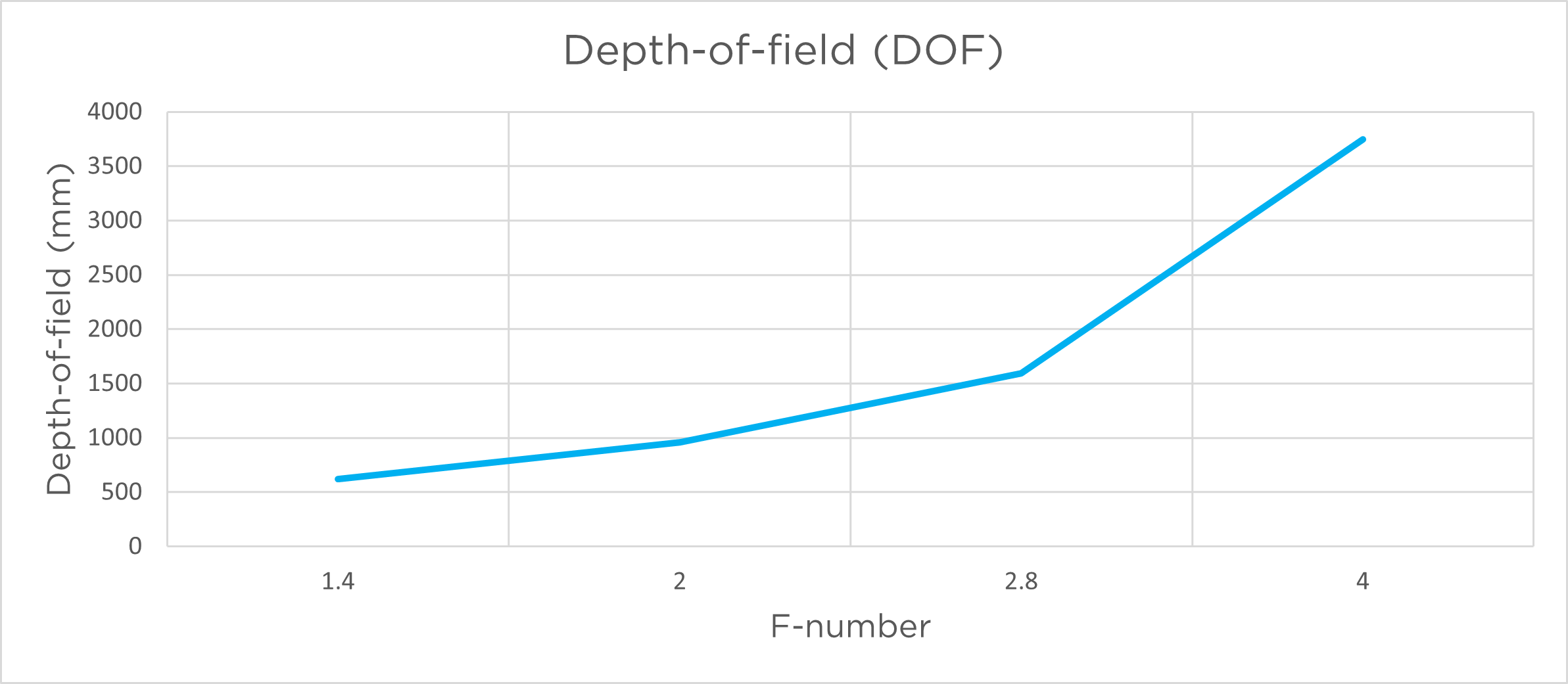
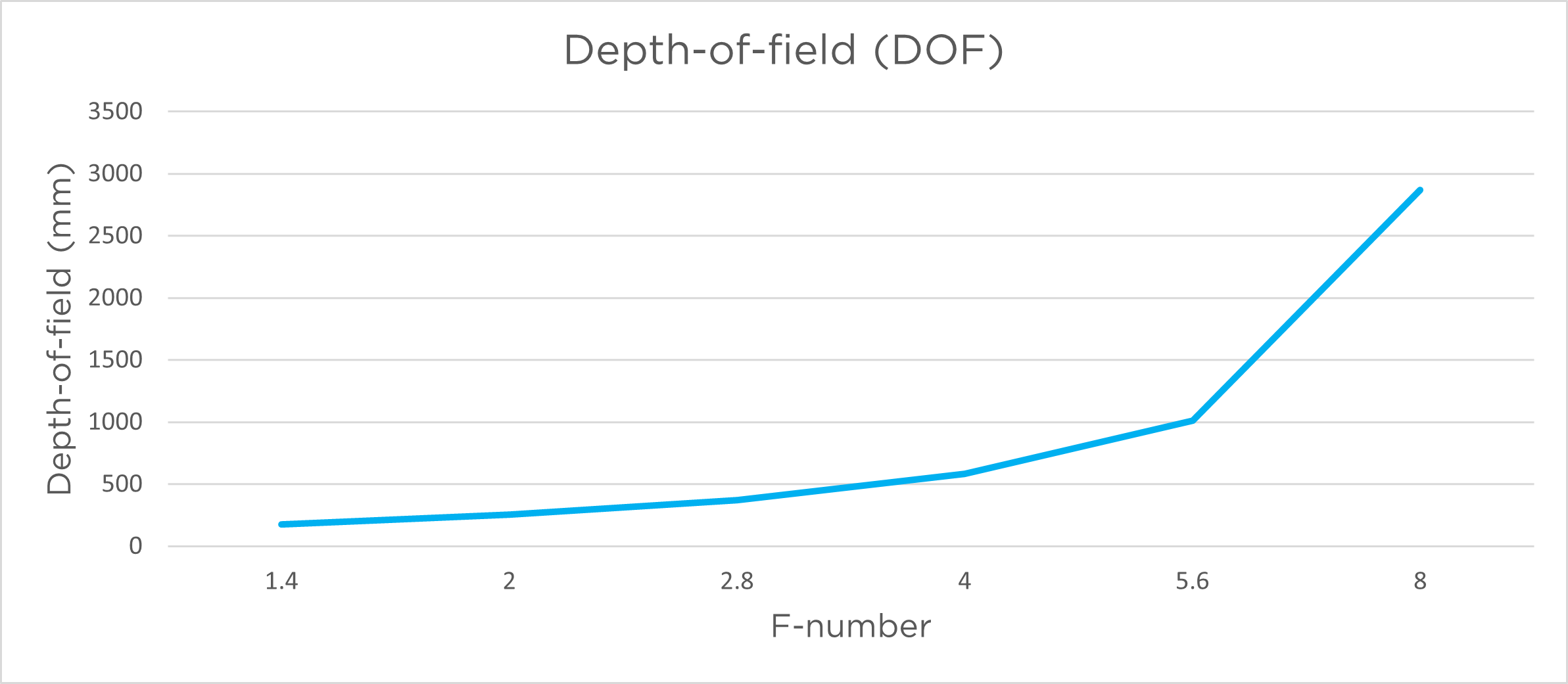
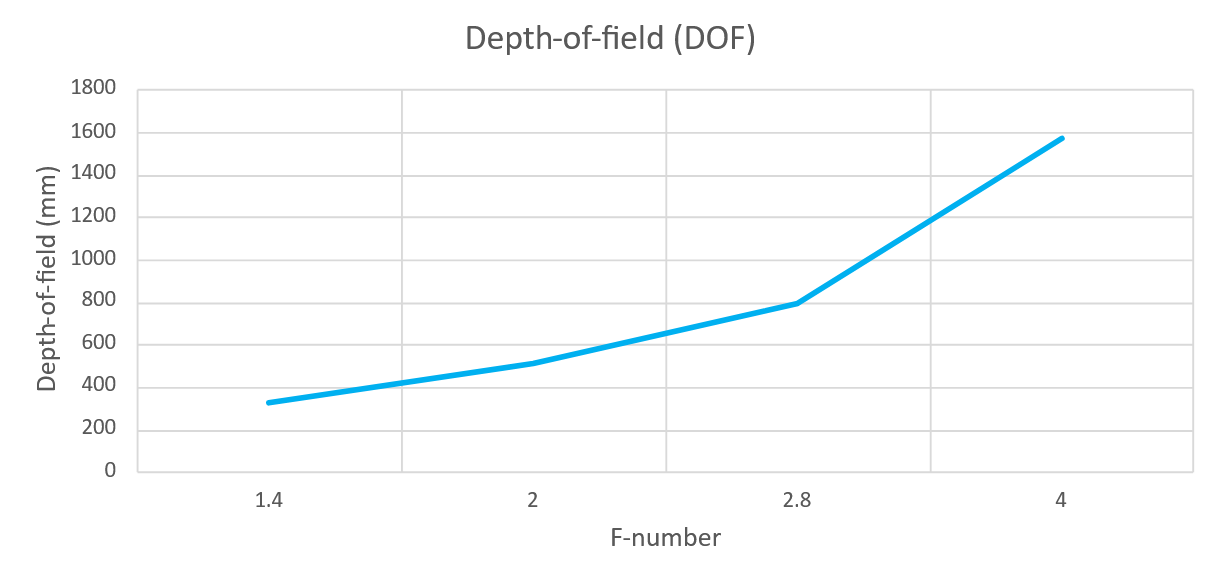
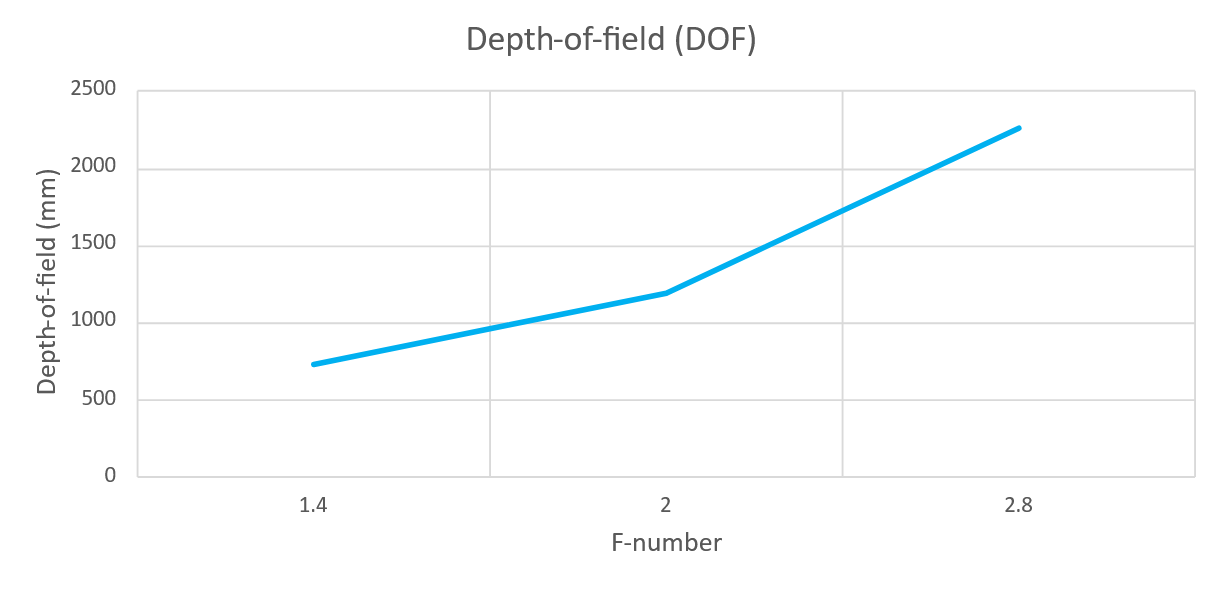
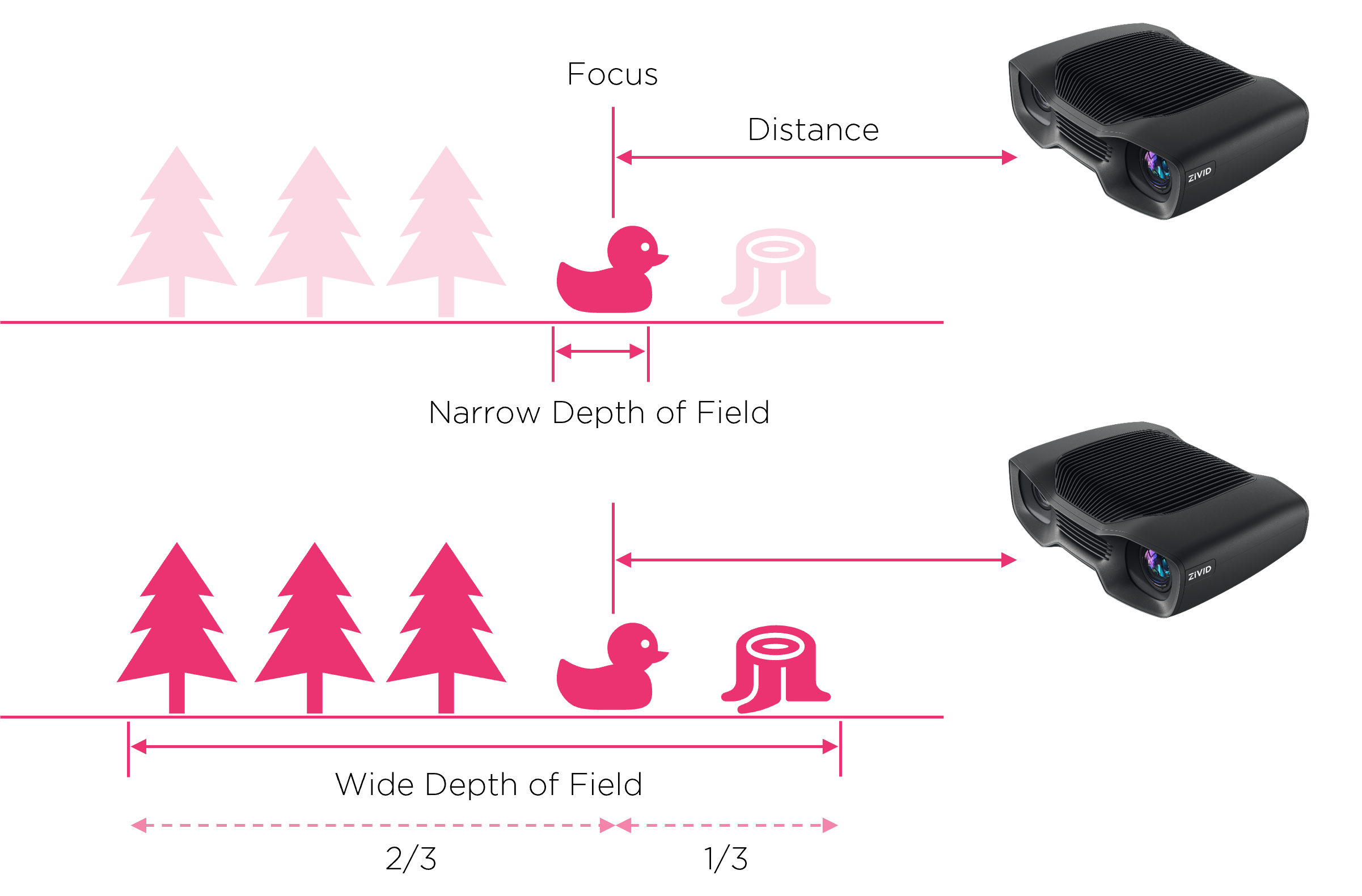
Depth of field is the image range that is in acceptably sharp focus for a given aperture. Wide aperture / iris (low f-number) gives a narrow depth of field (shorter focus range). Narrow aperture / iris (high f-number) gives a greater depth of field (longer focus range). Positioning of the DOF is around 1/3 in front and 2/3 behind focus point.
The graphs below show the depth of field as a function of aperture for Zivid cameras.
Further reading
Learn more about Depth of Focus.
Version History
SDK |
Changes |
|---|---|
2.0.0 |
Aperture API is changed from Iris to Aperture. See Porting guide for more info. |